Cryptographic Algorithms in BTC - ECDSA

In this article, we will discuss the ECDSA algorithm in BTC, and dive into the source code of btc to see how it works.

In blockchain, cryptographic plays an important role for the security of the network, one of the most important application is verify if a transations is from the owner of the account. One of the most popular cryptographic algorithms is Elliptic Curve Digital Signature Algorithm (ECDSA).

ECDSA algorithm

curve equation

First let’s talk about the Elliptic Curve. Elliptic Curve is a mathematical structure that is used to describe a set of points on a plane. The points on the curve are called EC points.

There is a curve equation that describes the relationship between the x and y values. the common equation is:

where p is the max value in case the computation is exceed the max value of the specific type size. while in btc world, the equation is named Secp256k1 and the curve parameters are:

curve operation

there is an operation in this curve. that is, given two point G and P on the curve, we can calculate the point Q, which is the sum of G and P. And this sum operation of the EC is not the normal arithmetic operation. it’s an operation that is called EC Addition. the operation is explained in the following picture:

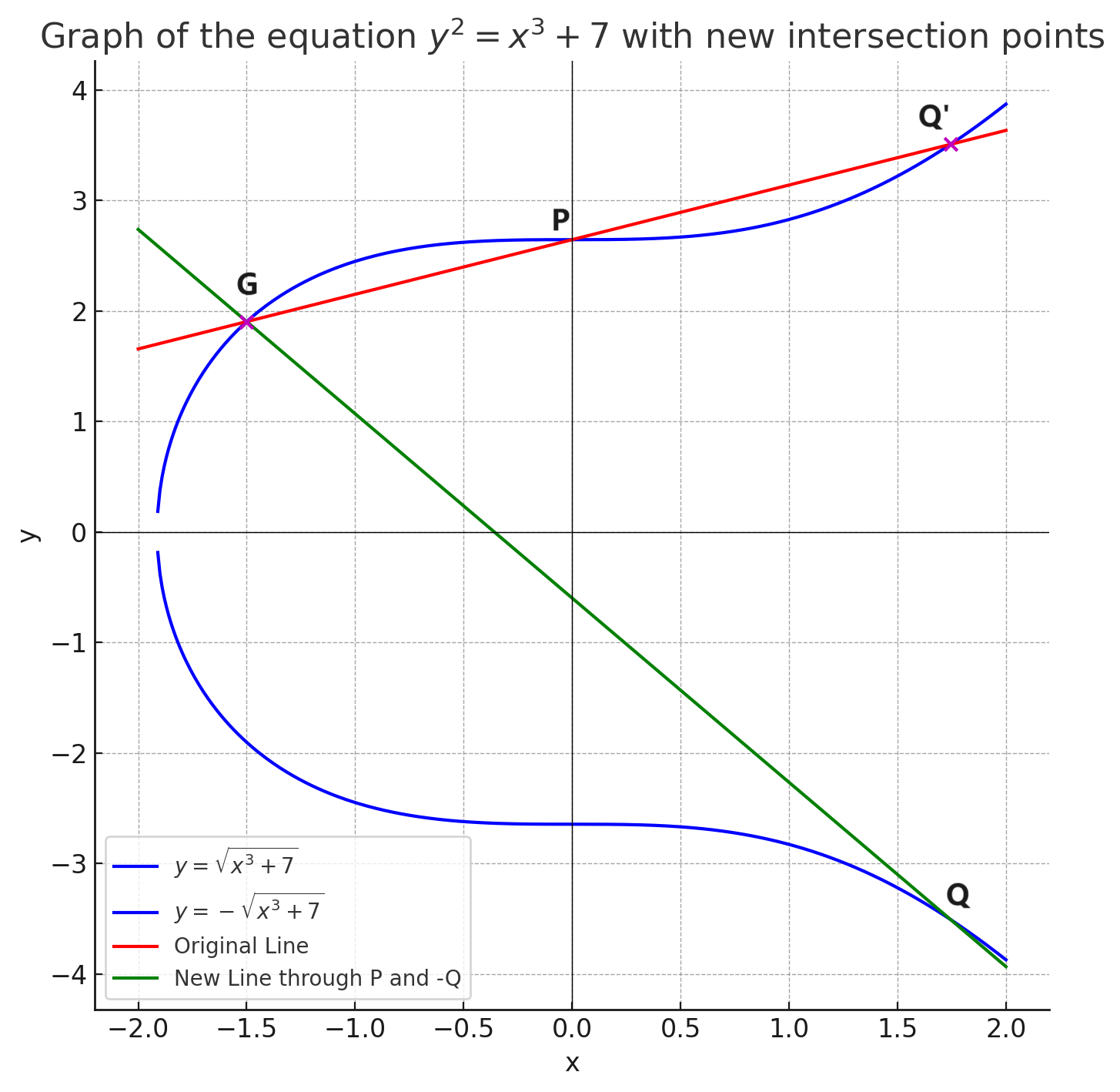the red line is line with the intersection points G(-1.5, 1.9) and P(0, 2.65)

the green line is line with the intersection points G(-1.5, 1.9) and Q

from the above pictures, we can see that the red line draw from G to P intersects the curve, assuming the intersection point is Q’(xq, yq), and the answer of G + P is Q(xq, -yq), that is G + P = Q, given the symmetrical features of the curve.

then we do that again with G, which is $G + Q = G + (G + P) = 2 \cdot G+P$. But the point is too far away, so we don’t show it here.

and we do that again and again, with a given times

$3 \cdot G + P$

$4 \cdot G + P$

$k \cdot G + P$

…

And this k is the private key, and we can use the same point from the beginning, where the line is the tangent to the curve at this point. We call this point as base point.

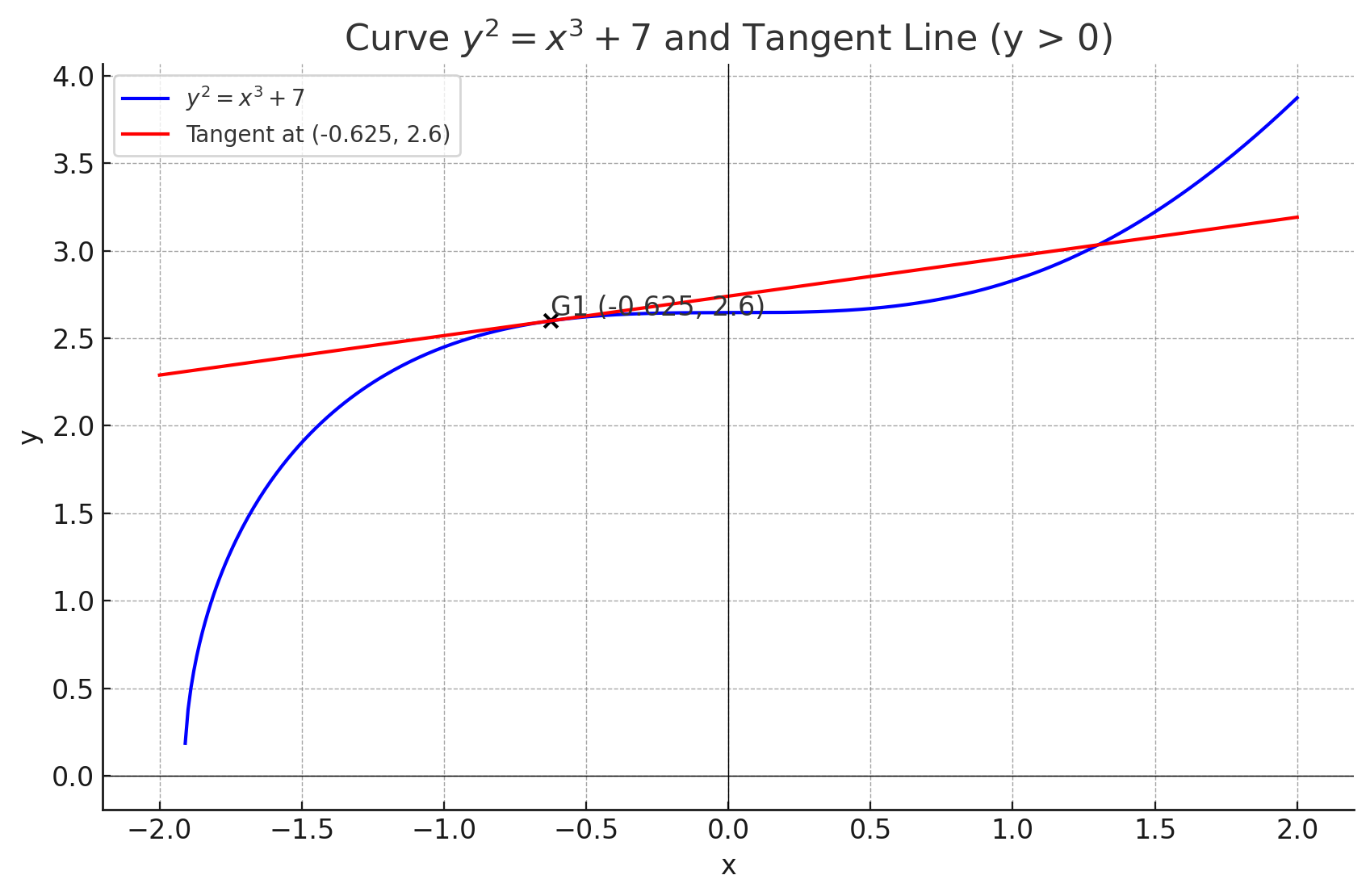
so now we have the final equation of the add operation $K = k \cdot G$

which is

Now you know how public key calculated by the private key. that is , At first, you will ge a random number from the range of 0 to n, and this number is the private key. And the public key is compute via the curve addition on the base point. And the base point is fixed.

Sign data

1. Hash the message $e=sha256(M)$
2. Generate $k$ randomly select $k$ from [1, n-1],
3. Compute $R$, $R = k \cdot G$, extract $r$, the x-coordinate of R, $r = R_x \bmod n$.
4. Compute $s$, $s= k^{-1}( e + d \cdot r)$, $d$ is the private key
5. The singnature is pair $(s, r)$

Verify data

1. Hash the message $e=sha256(M)$
2. compute $w$, $w = s^{-1}\bmod n$
3. compute $u_1$ and $u_2$, $u_1 = e \cdot w \bmod n$, $u_2 = r \cdot w \bmod n$
4. compute point $P$, $P= u_1 \cdot G + u_2 \cdot Q$, $Q$ is the public key
5. validate: Extract the x-coordinate of $P$ and check if it equals $s$, if the x-coordinate of P matches r, the signature is valid.

Math behind this equation

$P= u_1 \cdot G + u_2 \cdot Q = (e \cdot w) \cdot G + (r \cdot w) \cdot Q$

because Q is public key, so $Q = d \cdot G$, and then we have

$P= u_1 \cdot G + u_2 \cdot Q= (e \cdot w) \cdot G + (r \cdot w) \cdot (d \cdot G) = s^{-1}(e + r \cdot d) \cdot G $

with $s= k^{-1}( e + d \cdot r)$ , we have $k= s^{-1}( e + d \cdot r)$

finally, we have

$P = k \cdot G$, which is the same as R from the previous signature computation step.

so if the x-coordinate of P matches r, the signature is valid. And the verification only need the message $M$, the public key $Q$, the signature $s$ and $r$ (the x-coordinate of $R$).

btc source code

here is the verification function of ECDSA Signature in btc source code.

from the previous section we note that we only need the message $M$, the public key $Q$, the signature $s$ and $r$ (the x-coordinate of $R$) to verify the message.

and we can see that there is a equation $k \cdot s = ( e + d \cdot r)$

I clear the Exhaustive Tests and add comment to make it easier to understand.

static int secp256k1_ecdsa_sig_verify(const secp256k1_scalar *sigr, const secp256k1_scalar *sigs, const secp256k1_ge *pubkey, const secp256k1_scalar *message) {
    unsigned char c[32];
    secp256k1_scalar sn, u1, u2;

    secp256k1_fe xr;

    secp256k1_gej pubkeyj;
    secp256k1_gej pr;

    if (secp256k1_scalar_is_zero(sigr) || secp256k1_scalar_is_zero(sigs)) {
        return 0;
    }

    secp256k1_scalar_inverse_var(&sn, sigs); // w=s^-1
    secp256k1_scalar_mul(&u1, &sn, message); // u1 = e*w
    secp256k1_scalar_mul(&u2, &sn, sigr); // u2 = r*w
    secp256k1_gej_set_ge(&pubkeyj, pubkey); // Jacobian Coordinates of public key
    secp256k1_ecmult(&pr, &pubkeyj, &u2, &u1); // compute p = u1*G+u2*Q
    if (secp256k1_gej_is_infinity(&pr)) {
        return 0;
    }


    secp256k1_scalar_get_b32(c, sigr);

    (void)secp256k1_fe_set_b32_limit(&xr, c); // convert sigr to xr
    
    if (secp256k1_gej_eq_x_var(&xr, &pr)) { //Check xr Equality
        return 1;
    }
    ...

}